Given an m x n grid of characters board and a string word, return true ifword exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
m x n의 알파벳이 들어 있는 바둑판과 문자열이 주어진다, 만약 주어진 문자가 해당 바둑판에서 조합이 가능하다면 true를 리턴하라
단어는 인접한 셀의 조합으로 만들어진다, 인접한 셀은 가로, 세로로 인접한 셀들을 말한다.
같은 문자의 셀은 한번밖에 사용되지 않는다. ( 셀의 중복 사용 불가 )
먼저 주어진 바둑판에서 부터 문자열의 첫 번째 단어와 맞는 위치를 찾아야 한다.
찾아진 위치에서 부터 위, 아래, 오른쪽, 왼쪽을 방문하며 주어진 문자열에 존재하는 단어인지 비교한다.
비교한 단어가 같은 경우에는 해당 단어가 위치한 좌표를 방문한 노드로 표기하고 다시 위의 행위(찾아진 위치에서 부터 위, 아래, 오른쪽, 왼쪽을 방문하며 주어진 문자열에 존재하는 단어인지 비교)를 반복하여 전체 문자열을 찾는지 확인하면 된다.
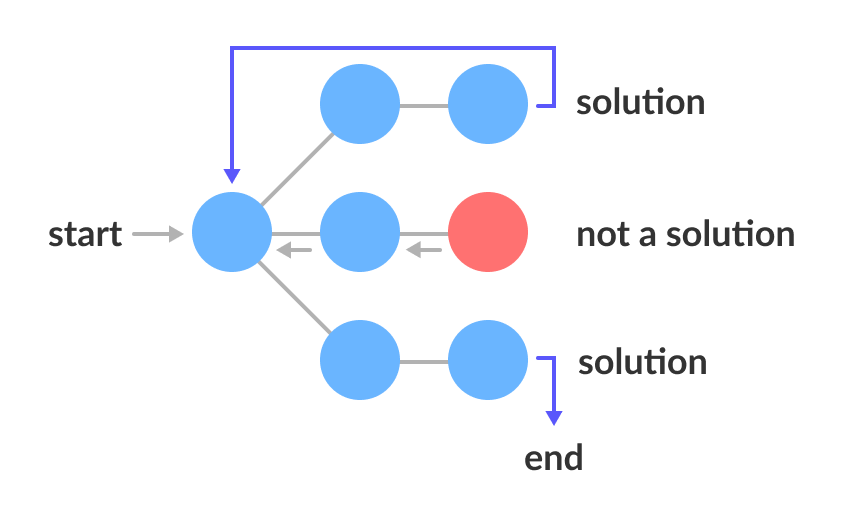
각각의 단어를 방문하는 부분을 Backtracking을 통해서 이미 방문한 위치이거나, 비교하려는 단어가 타깃이 아닌 경우에는 다시 뒤의 노드로 돌아가면 된다.
private boolean bt(char[][] board, int y, int x, String word, int idx, boolean[][] visited1) {
if (idx == word.length()) { //문자열의 모든 단어를 찾은 경우
return true;
}
int i = board.length;
int j = board[0].length;
if (x < 0 || x >= j) { // 조건이 맞지 않는 경우
return false;
}
if (y < 0 || y >= i) { // 조건이 맞지 않는 경우
return false;
}
if (visited1[y][x]) { // 조건이 맞지 않는 경우
return false;
}
if (word.charAt(idx) == board[y][x]) {
visited1[y][x] = true;
// 다음 노드들이 조건 맞는지 확인
boolean rst = bt(board, y - 1, x, word, idx + 1, visited1) ||
bt(board, y + 1, x, word, idx + 1, visited1)||
bt(board, y, x - 1, word, idx + 1, visited1) ||
bt(board, y, x + 1, word, idx + 1, visited1);
if (!rst) {
visited1[y][x] = false;
} else {
return true;
}
}
return false;
}
public boolean exist(char[][] board, String word) {
char start = word.charAt(0);
boolean[][] visited1 = new boolean[board.length][board[0].length];
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (board[i][j] == start) {
if (bt(board, i, j, word, 0, visited1)) {
return true;
}
}
}
}
return false;
}
출처 : https://leetcode.com/problems/word-search/
Word Search - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
'LeetCode' 카테고리의 다른 글
| [Leetcode][Java] 841 Keys and Rooms (열쇠와 방) (0) | 2021.07.22 |
|---|---|
| [Leetcode][Java] 101 Symmetric Tree (0) | 2021.07.07 |
| [Leetcode][Java] 46 Permutations (순열) (0) | 2021.06.09 |
| [Leetcode][Java] 78 Subsets (0) | 2021.06.06 |
| [Leetcode][Java] 322 Coin Change (동전 교환) (0) | 2021.05.14 |