기억하고싶은것들

위상 정렬(Topological Sorting)

순서가 정해져 있는 작업을 차례로 수행해야 할 때 그 순서를 결정해주는 데 사용되는 알고리즘

(일을 하는 순서를 찾는 알고리즘)

DAG( Directed Acyclic Graph ) -방향이 존재하고, 사이클이 존재하지 않는 그래프에서 사용 가능 

방향이 존재하는 그래프에서 사용하므로 

진입 차수를 사용하여 알고리즘을 구현한다.

진입 차수(indegree)

진입 차수(indegree) : 특정한 노드로 들어오는 간선의 개수

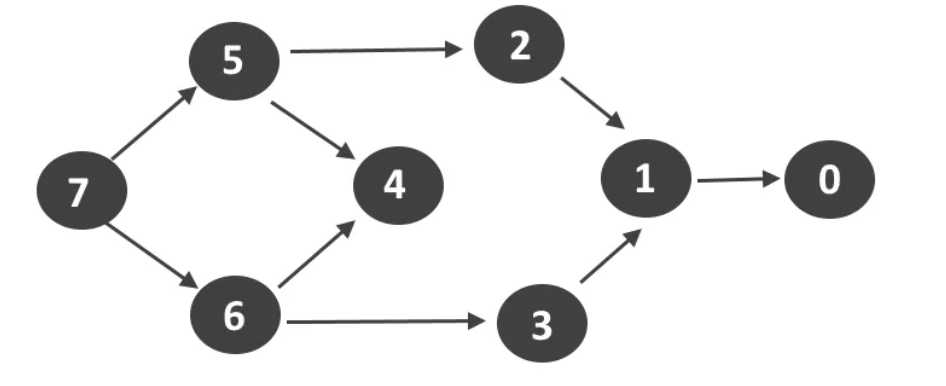
위의 그림에서 7 -> 5에서

5의 진입 차수는 1이다

7의 집입 차수는 0이다

위상 정렬 동작 과정

각 노드의 진입 차수를 구한다. 

진입 차수가 0 인 노드를 큐에 넣는다.

큐에 있는 노드의 간선을 제거 

 - ( 해당 간선을 진입 차수로 둔 노드의 진입 차수도 제거 )

 - 제거 과정에 진입 차수가 0이 된 노드는 큐에 추가 

    public boolean topologicalSorting(int numCourses, int[][] prerequisites) {

        List<Integer>[] graph = new ArrayList[numCourses];
        int[] inDegree = new int[numCourses];
        Queue<Integer> queue = new LinkedList<>();

        for (int i = 0; i < numCourses; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] pre : prerequisites) { // 노드별 진입차수 계산
            inDegree[pre[0]]++;
            graph[pre[1]].add(pre[0]);
        }
        for (int i = 0; i < inDegree.length; i++) { // 진입차수가 0인 노드 선별
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }

        while (!queue.isEmpty()) { // 큐의 노드 간선 제거 및 진입차수 제거 
            int idx = queue.poll();

            for (int tmp : graph[idx]) {
                inDegree[tmp]--;
                if (inDegree[tmp] == 0) {
                    queue.offer(tmp);
                }
            }
        }

        return Arrays.stream(inDegree).sum() == 0;
    }

관련 문제

https://leetcode.com/problems/course-schedule/

문자열 탐색 알고리즘

Rabin-Karp는 Hashing을 이용하여 문자열에서 특정 패턴과 일치하는지 찾는 알고리즘이다.

문자열에서 찾고자 하는 패턴의 길이만큼 hash값으로 변환하여, 패턴과 hash값이 같은지 확인을 하며

일치하지 않는 다면 한 칸씩 뒤로 이동하며 비교를 반복한다.

다만, hash값이 같다고 무조건 같은 패턴일 수는 없다.

그렇기 때문에 hash값이 같은 경우에는 문자열에 값과 패턴의 값을 일대일 매칭 하며 비교하는 과정도 필요하다.

기본적인 아이디어는 간단하다. 다만, 문자열을 이동하며 hash값을 계산해야 하는데 이 또한 효율적으로 찾을 수 있다. 

Rolling Hash

sliding window와 같이 문자열을 훑으면서 hash 값을 구하는데 유용하다.

주어진 문자열을 처음부터 끝까지 패턴과 비교하면서 해시값을 구하는데, 중복되는 부분의 해시값은 그대로 두고 업데이트되는 부분만 해시값을 계산해주어서 중복되는 연산을 줄일 수 있다.

위의 그림같은 경우에는 abec의 hash값 dece의 hash값을 구한다고 해보자

두 문자의 공통 부분인 dec는 그대로 두고 변경된 부분만 적용하면 된다.

우선 adec의 hash값은 

97*2^3 + 100*2^2 + 101*2^1 + 99*2^0 = 1477

다음으로 dece의 hash값은 아래와 같이 계산할 수 있다.

(1477 - 97*2^3) * 2 + 101*2^0 = 1503

adec문자에서 a는 제외되었기 때문에 a에 해당하는 값을 빼고 

한 자리씩 앞으로 이동했기 때문에 곱하기 2를 해주고 

마지막에 추가된 문자를 더해주면 된다.

    public List<Integer> find(String parent, String pattern) {

        int parentHash = 0, patternHash = 0, power = 1;

        int parentLen = parent.length();
        int patternLen = pattern.length();

        List<Integer> idxList = new ArrayList<>();

        for (int i = 0; i < parentLen - patternLen; i++) {

            if (i == 0) {
                for (int j = 0; j < patternLen; j++) {
                    parentHash = parentHash + parent.charAt(patternLen - 1 - j) * power;
                    patternHash = patternHash + pattern.charAt(patternLen - 1 - j) * power;

                    if (j < patternLen - 1) {
                        power *= 2;
                    }
                }
            } else {
                parentHash = (parentHash - parent.charAt(i - 1) * power) * 2 
                    + parent.charAt(i + patternLen - 1);
            }

            if (parentHash == patternHash) {
                boolean found = true;

                for (int j = 0; j < patternLen; j++) {
                    if (parent.charAt(i + j) != pattern.charAt(j)) {
                        found = false;
                        break;
                    }
                }

                if (found) {
                    idxList.add(i + 1);
                }
            }
        }

        return idxList;
    }

Quick Sort는 배열을 기반으로 동작하기 때문에 배열에 대한 기본적인 설명을 한다.

Array (배열)

Random Access 가능 

Backtracking, Dynamic Programming과 같은 문제와 조합하여 많이 나옴

2차원, n차원 배열과 조합되는 문제 - graph

배열과 단골 조합 문제 - Sorting

Stable Sort - Merge Sort ( 정렬 후 조건이 같은 케이스는 순서가 변하지 않는다)

Unstable Sort - Quick Sort ( 정렬 후, 조건이 같은 케이스라도 순서가 변할 수 있다)

배열과 단골 조합문제 - Search 

정렬이 되어있지 않은 경우 O(n)

정렬이 되어있는 경우 - O(logn) (binary search) 

Quick Sort 

핵심 키워드 pivot, partitioning

하나의 리스트를 pivot을 기준으로 두 개의 부분 리스트로 나눈다.

부분 리스트 중에 하나는 pivot보다 작은 값들이 모여있는 리스트

다른 하나는 pivot보다 큰 값들이 모여있는 리스트로 구성된다.

각각의 부분 리스트에 대해서 다시 재귀적으로 위의 동작을 반복한다.

(분할 정복 - Divide and Conquer)

    private void quicksort(int[] arr, int left, int right) {
        if (left < right) {
            int pivot = partition(arr, left, right);

            quicksort(arr, left, pivot - 1);
            quicksort(arr, pivot + 1, right);
        }
    }

    private int partition(int[] arr, int left, int right) {
        int low = left;
        int hight = right;

        int pivot = arr[left];

        while (low < hight) {
            while (arr[hight] > pivot && hight > low) {
                hight--;
            }

            while (arr[low] <= pivot && hight > low) {
                low++;
            }

            swap(hight, low, arr);
        }

        swap(left, low, arr);
        return low;
    }

    private void swap(int hight, int low, int[] arr) {
        int temp = arr[hight];
        arr[hight] = arr[low];
        arr[low] = temp;
    }

worst case - O(n*n)

best case - O(nlogn)

Tree의 종류 

Tree의 탐색 방법

Tree는 노드와 엣지의 연결관계를 나타낸다.

Root는 가장 상위의 노드를 나타내고, Leaf는 가장 하위의 노드를 나타낸다.

대부분의 알고리즘 문제에서 나오는 Tree는 Binary Tree로 자식이 2개 이하만 존재하는 Tree를 칭한다. 

Binary Tree의 종류

Full Binary Tree

각각의 노드가 Child가 없거나 2개의 Child를 가지는 경우

Complete Binary Tree

왼쪽(Left)에서 부터 가득 차있는 경우

Perfect Binary Tree

모든 노드들이 2개의 Child를 가지고 있고 Leaf의 Level이 모두 같은 경우

Tree의 탐색 종류

PreOrder : N->L->R 

( 가운데 노드가 가장 먼저 나온다 ) 

InOrder : L->N->R

( 가운데 노드가 중간에 나온다 )

PostOrder : L->R->N

( 가운데 노드가 가장 마지막에 나온다 )

Recursive를 이용해 Tree 탐색 구현해보기 ( PreOrder )

	public static void main(String[] args) {
		
		TreeNode n1 = new TreeNode(1);
        
        // ... TreeNode 구성 
        
		System.out.println("PreOrder");
		recursivePreOrder(n1);
	}

	private static void recursivePreOrder(TreeNode n) {
		
		if (Objects.isNull(n)) {
			return;
		}
		
		System.out.print(n.val + " - ");
		
		recursivePreOrder(n.left);
		recursivePreOrder(n.right);
		
	}

Iterative를 이용해 Tree 탐색 구현해보기 ( PreOrder )

	private static void iterativePreOrder(TreeNode n) {
		
		if (Objects.isNull(n)) {
			return;
		}
		
		Stack<TreeNode> stack = new Stack<>();
		stack.push(n);
		
		while (stack.size() > 0) {
			TreeNode tmp = stack.pop();
			System.out.print(tmp.val + " - ");
			
			if(Objects.nonNull(tmp.right)) {
				stack.push(tmp.right);
			}
			
			if(Objects.nonNull(tmp.left)) {
				stack.push(tmp.left);
			}
		}
	}