SMALL
Tree의 종류
Tree의 탐색 방법
Tree는 노드와 엣지의 연결관계를 나타낸다.
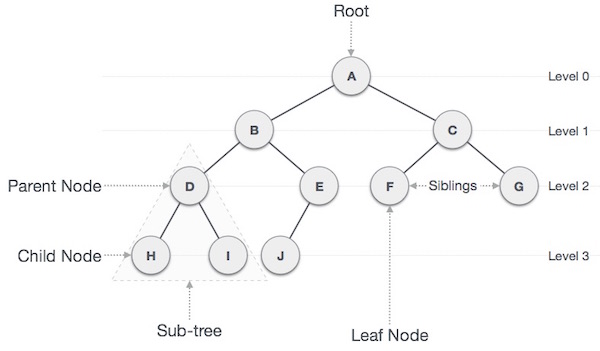
Root는 가장 상위의 노드를 나타내고, Leaf는 가장 하위의 노드를 나타낸다.
대부분의 알고리즘 문제에서 나오는 Tree는 Binary Tree로 자식이 2개 이하만 존재하는 Tree를 칭한다.
Binary Tree의 종류
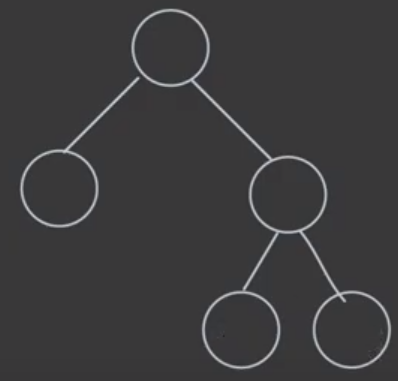
Full Binary Tree
각각의 노드가 Child가 없거나 2개의 Child를 가지는 경우
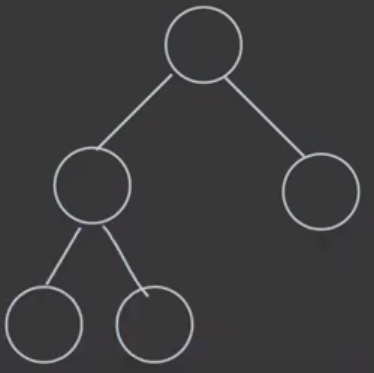
Complete Binary Tree
왼쪽(Left)에서 부터 가득 차있는 경우
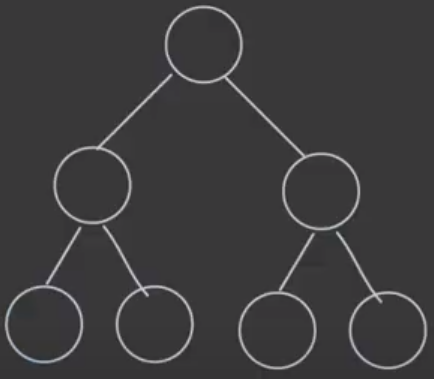
Perfect Binary Tree
모든 노드들이 2개의 Child를 가지고 있고 Leaf의 Level이 모두 같은 경우
Tree의 탐색 종류
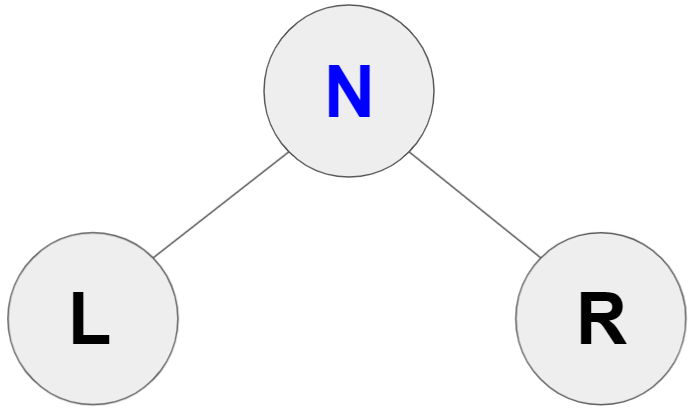
PreOrder : N->L->R
( 가운데 노드가 가장 먼저 나온다 )
InOrder : L->N->R
( 가운데 노드가 중간에 나온다 )
PostOrder : L->R->N
( 가운데 노드가 가장 마지막에 나온다 )
Recursive를 이용해 Tree 탐색 구현해보기 ( PreOrder )

public static void main(String[] args) {
TreeNode n1 = new TreeNode(1);
// ... TreeNode 구성
System.out.println("PreOrder");
recursivePreOrder(n1);
}
private static void recursivePreOrder(TreeNode n) {
if (Objects.isNull(n)) {
return;
}
System.out.print(n.val + " - ");
recursivePreOrder(n.left);
recursivePreOrder(n.right);
}
Iterative를 이용해 Tree 탐색 구현해보기 ( PreOrder )
private static void iterativePreOrder(TreeNode n) {
if (Objects.isNull(n)) {
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(n);
while (stack.size() > 0) {
TreeNode tmp = stack.pop();
System.out.print(tmp.val + " - ");
if(Objects.nonNull(tmp.right)) {
stack.push(tmp.right);
}
if(Objects.nonNull(tmp.left)) {
stack.push(tmp.left);
}
}
}
LIST
'Algorithm' 카테고리의 다른 글
| [알고리즘] 라빈 카프(Rabin-Karp)(문자열 탐색)(Rolling Hash) (0) | 2022.01.31 |
|---|---|
| [알고리즘] Quick Sort (0) | 2021.12.15 |
| [알고리즘] Backtracking ( 백트래킹, 퇴각 검색 ) (0) | 2021.06.03 |
| [알고리즘] Dynamic Programming ( 동적 계획법 ) (0) | 2021.04.17 |
| [알고리즘] Flood Fill ( Seed Fill ) (0) | 2021.03.27 |