기억하고싶은것들

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

계단을 올라보자. input으로 n을 받고 해당 값은 맨 위로 가기 위한 스텝의 개수이다.

각각 1 또는 2개의 계단만 오를 수 있다. 몇가지 방법으로 맨 위로 올라갈 수 있는지 구해라

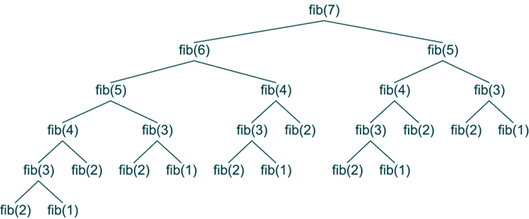
해당 문제에서 n까지 도달하기 위한 방법은, 유저가 올라 갈 수 있는 계단의 개수는 1 또는 2 이므로,

f(n) = f(n-1) + fn-2) 로 표현될 수 있다.

이러한 형태의 문제는 dynamic programming을 통해서 해결될 수 있다.

추가적으로, 방문 했던 위치는 해당 위치로 올 수 있는 개수를 따로 저장해 두고 또 방문했을 때 재 계산을 하지 않고 저장된 값을 불러서 사용하면 된다. 

먼저, 위의 식 처럼 해결할 수 있는 Top-Down 방식을 보자. 

    private int df(int n, int[] t) {
        if (n == 1) {
            return 1;
        }
        if (n == 0) {
            return 1;
        }
        if (t[n] != 0) {
            return t[n];
        }
        int n1 = df(n - 1, t);
        int n2 = df(n - 2, t);
        t[n] = n2 + n1;
        return n1 + n2;
    }

그럼 해당 코드를 호출하는 부분을 보자

    public int climbStairs(int n) {
        int[] t = new int[n + 1];
        t[0] = 1;
        t[1] = 1;
        int rst = df(n, t);
        return rst;
    }

그럼, 다음으로 Bottom-Up 방식을 보자

    public int climbStairs(int n) {
        int[] t = new int[n];
        t[0] = 1;
        t[1] = 1;
        for (int i=2; i<n; i++) {
        t[i] = t[i-1] + t[i-2];
        }
        return t[n-1];
    }

문제 출처 :

leetcode.com/problems/climbing-stairs/

Let's play the minesweeper game (Wikipedia, online game)!

You are given a 2D char matrix representing the game board. 'M' represents an unrevealedmine, 'E' represents an unrevealed empty square, 'B' represents a revealed blank square that has no adjacent (above, below, left, right, and all 4 diagonals) mines, digit ('1' to '8') represents how many mines are adjacent to this revealed square, and finally 'X' represents a revealed mine.

Now given the next click position (row and column indices) among all the unrevealed squares ('M' or 'E'), return the board after revealing this position according to the following rules:

1. If a mine ('M') is revealed, then the game is over - change it to 'X'.
2. If an empty square ('E') with no adjacent mines is revealed, then change it to revealed blank ('B') and all of its adjacent unrevealed squares should be revealed recursively.
3. If an empty square ('E') with at least one adjacent mine is revealed, then change it to a digit ('1' to '8') representing the number of adjacent mines.
4. Return the board when no more squares will be revealed.

지뢰 찾기 게임을 플레이하자!

2차원의 char 배열이 주어진다.

• 'M'은 플레이어가 지뢰라고 표시해 놓은 칸
• 'E'는 눌러지지 않는 칸
• 'B'는 아무것도 없는 칸
• '숫자'는 주변에 인접한 지뢰의 개수
• 'X'는 지뢰 

다음으로, 누를 지점의 값을 input으로 입력을 받는다

그 후에 2차원 char 배열의 결과를 반환하라.

1. 만약, 'M'이 눌리면 'X'로 변환하고 게임 끝
2. 만약, 주변에 지뢰가 하나도 없는 'E'가 눌리면, 'B'로 바뀌고 해당 인접한 칸의 값을 변환
3. 만약, 주변에 지뢰가 하나 이상 있는 'E'가 눌리면, 숫자로 바꾼다.
4. 더 이상 표현할 수 있는 칸이 없을 때 2차원 배열을 반환하라

지뢰 찾기는 주변에 인접한 칸들을 방문하며 문제를 풀어가는 특징이 있다.

이러한 문제는 기존에 Graph의 Level (인접한 레벨) 별로  방문하는 BFS로 해결할 수 있다.

graph에서는 자신의 child를 방문했다면, 2차원의 배열에서는 자신에 인접한 칸들을 방문하면 된다. 

int [] dx = new int[] { 0, -1, 0, 1, 1, -1, 1, -1 };
int[] dy = new int[] { 1, 0, -1, 0, 1, -1, -1, 1 };

주변에 인접한 칸들이 방문 가능한 칸인지 판별하고, 방문이 가능하다면 queue에 담아서 순차적으로 방문을 하면 된다. 

또한, 중복적으로 방문한 칸을 들리지 않기 위해서 방문한 칸들을 기록하는 2차원의 배열을 두면 무한 반복을 막을 수 있다.

    public char[][] updateBoard(char[][] board, int[] click) {

        if (board[click[0]][click[1]] == 'M') {
            board[click[0]][click[1]] = 'X';
            return board;
        }

        Queue<int[]> queue = new LinkedList<>();
        boolean[][] visited = new boolean[board.length][board[0].length];

        queue.offer(click);
        visited[click[0]][click[1]] = true;

        while (!queue.isEmpty()) {
            int[] cur = queue.poll();
            int x = cur[0], y = cur[1];
            int mines = getNumberOfMines(board, x, y);

            if (mines == 0) {
                board[x][y] = 'B';

                for (int i = 0; i < 8; i++) {
                    int nx = x + dx[i], ny = y + dy[i];
                    // Check adjacent cell visitable or not 
                    if (nx >= 0 && ny >= 0 && nx < board.length && ny < board[0].length && !visited[nx][ny]) {
                        queue.offer(new int[] { nx, ny });
                        visited[nx][ny] = true; // Check this cell visited 
                    }
                }
            } else {
                board[x][y] = (char) (mines + '0');
            }
        }

        return board;
    }

추가적으로, 해당 셀 주변에 지뢰가 몇 개 있는지 판별하는 메서드를 따로 두었다.

    private int getNumberOfMines(char[][] board, int x, int y) {
        int cnt = 0;
        for (int i = 0; i < 8; i++) {
            int nx = x + dx[i], ny = y + dy[i];
            if (nx >= 0 && ny >= 0 && nx < board.length && ny < board[0].length) {
                cnt += board[nx][ny] == 'M' ? 1 : 0;
            }
        }
        return cnt;
    }

문제 출처 :

leetcode.com/problems/minesweeper/

• dynamic programming에 대한 개념 설명
• dynamic programming을 적용하기 위한 조건 
• dynamic programming의 특징
• dynamic programming의 접근법

Dynamic Programming은 보통 DP라고 줄여 쓰는것을 볼 수 있다.

이름만 봤을때는 뭔가 엄청나게 대단하고 복잡한 알고리즘일것 같은데, 실제 해당 내역을 공부하면 이름이랑 뭔가 맞지 않는다는게 느껴진다.

보통 인터넷을 찾아봤을때, Dynamic Programming의 정의는 아래와 같다.

복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법 

개념은 그렇게 어렵지 않고, 받아들일수 있다.

그러면, 이러한 DP를 어떠한 상황에 적용할 수 있는지 알아보자.

가장 대표적인 예시로는 피보나치 수열이 있다. 

간단하게 피보나치 수열에 대한 정의를 보면 아래와 같다.

첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열 이다.
처음 여섯 항은 각각 (0), 1, 1, 2, 3, 5, 8이다.
편의상 0번째 항을 0으로 두기도 한다.

DP라는 개념이 등장하기 전에는 대부분 해당 문제를 재귀적으로 해결하였다. 

아래는 예시 코드이다.

int fibonacci(int n) {
    if (n<=2)
      return 1;
    else
      return fibonacci(n-1) + fibonacci(n-2);
}

하지만 해당 방법으로 문제를 풀게 된다면, 반복되는 값들을 반복적으로 구한다는 문제가 있다. 

아래의 그림에서 트리에서 반복적으로 fib(5) 이하의 노드들을 계산하게 된다. 

한번만 계산해 놓고 해당 값을 다시 만나면 이전에 계산해 놓은 값을 가져다가 쓰기만 하면 계산 시간을 효율적으로 줄일 수 있게된다.

이러한 점을 반영하여서 DP의 적용 조건과 특징을 살펴보자.

DP의 적용 조건

• 부분문제 반복 ( Overlapping Subproblem )
  • 피보나치 수열과 같이  f(n) = f(n-1) + f(n-2) 와 같이 
    어떠한 문제가 여러개의 부분 문제로 쪼개 질 수 있고, 해당 부분 문제가 또 다시  재귀적으로 부분 문제로 쪼개질 수 있는 것
• 최적 부분구조 ( Optimal Substructure )
  • 피보나치 수열과 같이 f(n) = f(n-1) + f(n-2)와 같이
    작은 부분 문제에서 구한 최적의 답으로 합쳐진 큰 문제의 최적의 답을 구할 수 있는 것

( 해당 조건은 뭔가 전문적인 단어들이 들어가서 어렵게 표현된 것처럼 보이는데, DP의 핵심은 "복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 것" 이다. 이 핵심을 풀어서 전문적으로 설명해 놓은게 조건이라고 생각하자.)

DP의 특징으로는 Memorization이다.

반복적으로 등장하는 계산을 기억해 두었다가, 해당 계산이 다시 등장할때, 재계산을 하지 않고 기억해 두었던 값을 가져다 사용하는 것이다. 

위의 피보나치 수열 그래프에서 반복적으로 등장하는 fibo(5), fibo(4) ... 값들을 기억하고 사용하면 된다. 

접근법

이제 개념적인 부분과 특징을 알아 보았으니 실제로 문제를 만났을때 어떻게 접근해야하는지에 대해서 알아보도록 하자.

크게 2가지 방법이 있다. 

• Top-Down
  • 재귀로 해결 하는 대부분의 방식
  • 큰 문제를 해결 하기 위해 작은 문제로 나누고, 해당 값이 아직 계산되지 않은 경우 더 작은 값으로 나누며 값을 찾아가는 방식
  • ( 예시는 위의 fibonacci 코드 )
• Botton-up
  • 작은 문제에서 부터 하나씩, 하나씩 값을 찾아가는 방식
  • ( 예시는 아리의 코드 )

int fibonacci (int n) {
  fibodata[0] = 0;
  fiboData[1] = 1;
  for (int i=2; i<=n; i++) {
    fiboData[i] = fiboData[i - 1] + fiboData[i - 2];
  }
  return fiboData[n];
}

Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).

이진트리의 루트가 주어지고, 트리의 각 레벨의 가장 큰 값들을 담은 배열을 반환해라. ( 0부터 시작 )

해당 문제에서는 트리의 레벨 별로 특정한 값을 찾는 문제 이므로, 트리의 레벨별로 그래프를 순환하는 bfs를 사용하여 문제를 해결해 보자.

    public List<Integer> largestValues(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        List<Integer> rst = new ArrayList<>();
        if (root == null) { // Check Input is Null
            return rst;
        }
        
        queue.add(root); 
        while (!queue.isEmpty()) { // Check by Tree Level
            int size = queue.size();
            int max = Integer.MIN_VALUE;

            for (int i = 0; i < size; i++) { // Only Rotate Level Node 
                TreeNode temp = queue.poll();
                if (temp.val > max) {
                    max = temp.val;
                }

                if (temp.right != null) {
                    queue.add(temp.right);
                }
                if (temp.left != null) {
                    queue.add(temp.left);
                }
            }
            rst.add(max);
        }
        return rst;
    }