기억하고싶은것들

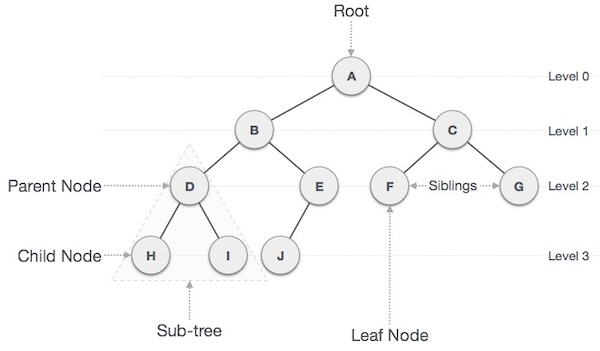
JPA를 이용한다면 일반적인 테이블 간의 관계를 이용하는 것처럼, 

Entity 사이의 관계를 통해 데이터를 관리할 수 있다.

하지만, JPA를 사용하여 연관관계를 맺기 위해서는 참조 변수를 이용하기 때문에

테이블의 연관과 Entity의 연관이 정확하게 일치하지 않는다.

이러한 문제를 해결하면서 연관관계를 매핑하는 방법을 알아야 한다.

먼저, 연관관계 매핑에 사용되는 용어들을 정리해 보자.

방향 (Direction)

단방향 관계: 두 Entity가 관계를 맺을 때, 한쪽의 Entity만 참조하고 있는 것을 의미한다
양방향 관계: 두 Entity가 관계를 맺을 때, 양쪽이 서로 참조하고 있는 것을 의미한다

다중성 (Multiplicity)

Many To One: 다대일 (N : 1)
One To Many: 일대다 (1 : N)
One To One: 일대일 (1 : 1)
Many To Many: 다대다 (N : N)

위의 관계 중에 일대다(1 : N)와 다대일(N : 1)은 같은 것이라고 생각할 수 있다.

예를 들어, 유저가 게시판에 등록하는 글의 관계를 보면 

유저는 여러개의 글을 등록할 수 있어 : 유저와 게시판의 관계는 일대다(1 : N)

게시판에는 여러 유저가 등록한 글이 존재하므로 : 게시판과 유저의 관계는 다대일(N : 1)

어떻게 생각하면 같은 것인데, 중요하게 중점을 두어야 하는 것은

"어떤 Entity를 중심으로 상대 Entity를 바라보느냐" 이다.

연관 관계의 주인 (Owner)

Entity 사이의 관계에서의 주인을 찾는 방법은 

연관관계를 갖는 두 테이블에 대해서 외래 키(Foreign Key)를 갖는 테이블이 연관관계의 주인이 된다.

연관관계의 주인만이 외래 키(Foreign Key)를 관리할 수 있고, 반면 주인이 아닌 Entity는 읽기만 할 수 있다.

( 결국 Entity의 관계를 생각할 때는 이미 설계된 테이블의 내역을 기반으로 관계를 그리는 게 더 이해하기 쉬운 거 같다)

( 그렇기 때문에 데이터베이스에 대한 지식과 학습이 필요하다고 느껴진다.. ㅎㅎ)

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

이진트리의 루트가 주어진다. 해당 트리의 좌우가 대칭인지 확인하여라 

이 문제는 주어진 트리가 대칭인지 판단하는 문제로, 트리를 순환하며 값을 비교해야 한다.

트리를 순환하는 방법은 크게 Iterative, Recursive와 같이 두 가지 방법이 존재한다.

이 두개의 방법을 모두 사용한 예시 코드를 각각 보도록 하자.

우선 iterative 한 방법을 보자 

해당 예시에서는 Stack을 사용하였다.

    public boolean isSymmetric_iterative(TreeNode root) {

        Stack<TreeNode> tree = new Stack<>(); // right side stack
        Stack<TreeNode> mirror = new Stack<>(); // left side stack

        tree.push(root.right);
        mirror.push(root.left);

        while (tree.size() > 0 && mirror.size() > 0) {
            TreeNode treetemp = tree.pop();
            TreeNode mirrortemp = mirror.pop();

            if (treetemp == null && mirrortemp == null) {
                continue;
            }

            if (treetemp == null || mirrortemp == null) {
                return false;
            }

            if (treetemp.val != mirrortemp.val) {
                return false;
            }

            tree.push(treetemp.left);
            mirror.push(mirrortemp.right);

            tree.push(treetemp.right);
            mirror.push(mirrortemp.left);

        }

        return true;
    }

오른쪽과 왼쪽의 노드의 대칭을 비교하기 위해서 두 개의 Stack을 이용하였다.

각각의 Stack에는 서로 대칭되는 값을 넣는다

( right에 해당하는 stack에 right node를 넣는다면, left에 해당하는 stack에는 left node를 넣는다)

그럼 다음으로 Recursive한 방법으로 주어진 트리가 대칭인지 확인하는 예시 코드를 보자

    public boolean isSymmetric_recursive(TreeNode root) {

        TreeNode right = root.right;
        TreeNode left = root.left;

        return recursive(right, left);
    }

    private boolean recursive(TreeNode right, TreeNode left) {

        if (right == null && left == null) {
            return true;
        }

        if (right == null || left == null) {
            return false;
        }

        boolean valRst = right.val == left.val;
        boolean rRst = recursive(right.right, left.left);
        boolean lRst = recursive(right.left, left.right);

        return valRst && rRst && lRst;
    }

이 방법에서는 recursive 함수를 호출시, 오른쪽 왼쪽 노드의 값을 전달하여 비교하는 방식을 취한다.

그리고 결과는 각 노드의 값 비교 및 오른쪽 recursive 및 왼쪽 recursive의 조건을 and로 묶어 결과를 반환한다

( 해당 결과 모두 true 여야 대칭이 만족 )

Spring Boot Admin에서 기본적으로 타겟 client의 application.properties 설정값을 조회할 수 있다.

그럼 다음으로 해당 설정 값을 바꿀 수 있는 방법에 대해서 알아보자.

pom.xml ( dependency 설정 )

		<dependency>
			<groupId>org.springframework.cloud</groupId> 
			<artifactId>spring-cloud-context</artifactId>
		</dependency>

application.properties ( spring boot 설정 )

management.endpoint.env.post.enabled=true

위의 설정들을 추가하면 아래와 같이 해당 화면의 설정할 수 있는 부분이 생기게 된다. 

Tree의 종류 

Tree의 탐색 방법

Tree는 노드와 엣지의 연결관계를 나타낸다.

Root는 가장 상위의 노드를 나타내고, Leaf는 가장 하위의 노드를 나타낸다.

대부분의 알고리즘 문제에서 나오는 Tree는 Binary Tree로 자식이 2개 이하만 존재하는 Tree를 칭한다. 

Binary Tree의 종류

Full Binary Tree

각각의 노드가 Child가 없거나 2개의 Child를 가지는 경우

Complete Binary Tree

왼쪽(Left)에서 부터 가득 차있는 경우

Perfect Binary Tree

모든 노드들이 2개의 Child를 가지고 있고 Leaf의 Level이 모두 같은 경우

Tree의 탐색 종류

PreOrder : N->L->R 

( 가운데 노드가 가장 먼저 나온다 ) 

InOrder : L->N->R

( 가운데 노드가 중간에 나온다 )

PostOrder : L->R->N

( 가운데 노드가 가장 마지막에 나온다 )

Recursive를 이용해 Tree 탐색 구현해보기 ( PreOrder )

	public static void main(String[] args) {
		
		TreeNode n1 = new TreeNode(1);
        
        // ... TreeNode 구성 
        
		System.out.println("PreOrder");
		recursivePreOrder(n1);
	}

	private static void recursivePreOrder(TreeNode n) {
		
		if (Objects.isNull(n)) {
			return;
		}
		
		System.out.print(n.val + " - ");
		
		recursivePreOrder(n.left);
		recursivePreOrder(n.right);
		
	}

Iterative를 이용해 Tree 탐색 구현해보기 ( PreOrder )

	private static void iterativePreOrder(TreeNode n) {
		
		if (Objects.isNull(n)) {
			return;
		}
		
		Stack<TreeNode> stack = new Stack<>();
		stack.push(n);
		
		while (stack.size() > 0) {
			TreeNode tmp = stack.pop();
			System.out.print(tmp.val + " - ");
			
			if(Objects.nonNull(tmp.right)) {
				stack.push(tmp.right);
			}
			
			if(Objects.nonNull(tmp.left)) {
				stack.push(tmp.left);
			}
		}
	}