SMALL
Quick Sort는 배열을 기반으로 동작하기 때문에 배열에 대한 기본적인 설명을 한다.
Array (배열)
Random Access 가능
Backtracking, Dynamic Programming과 같은 문제와 조합하여 많이 나옴
2차원, n차원 배열과 조합되는 문제 - graph
배열과 단골 조합 문제 - Sorting
Stable Sort - Merge Sort ( 정렬 후 조건이 같은 케이스는 순서가 변하지 않는다)
Unstable Sort - Quick Sort ( 정렬 후, 조건이 같은 케이스라도 순서가 변할 수 있다)
배열과 단골 조합문제 - Search
정렬이 되어있지 않은 경우 O(n)
정렬이 되어있는 경우 - O(logn) (binary search)
Quick Sort
핵심 키워드 pivot, partitioning
하나의 리스트를 pivot을 기준으로 두 개의 부분 리스트로 나눈다.
부분 리스트 중에 하나는 pivot보다 작은 값들이 모여있는 리스트
다른 하나는 pivot보다 큰 값들이 모여있는 리스트로 구성된다.
각각의 부분 리스트에 대해서 다시 재귀적으로 위의 동작을 반복한다.
(분할 정복 - Divide and Conquer)
private void quicksort(int[] arr, int left, int right) {
if (left < right) {
int pivot = partition(arr, left, right);
quicksort(arr, left, pivot - 1);
quicksort(arr, pivot + 1, right);
}
} private int partition(int[] arr, int left, int right) {
int low = left;
int hight = right;
int pivot = arr[left];
while (low < hight) {
while (arr[hight] > pivot && hight > low) {
hight--;
}
while (arr[low] <= pivot && hight > low) {
low++;
}
swap(hight, low, arr);
}
swap(left, low, arr);
return low;
} private void swap(int hight, int low, int[] arr) {
int temp = arr[hight];
arr[hight] = arr[low];
arr[low] = temp;
}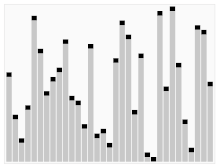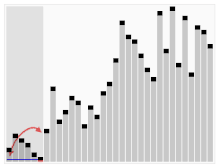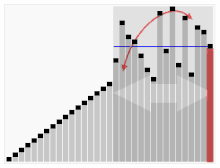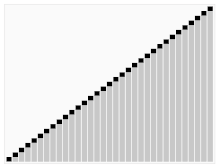
worst case - O(n*n)
best case - O(nlogn)
LIST
'Algorithm' 카테고리의 다른 글
| [알고리즘] 위상 정렬(Topological Sorting) 이란 (0) | 2022.03.28 |
|---|---|
| [알고리즘] 라빈 카프(Rabin-Karp)(문자열 탐색)(Rolling Hash) (0) | 2022.01.31 |
| [알고리즘] Tree (0) | 2021.06.25 |
| [알고리즘] Backtracking ( 백트래킹, 퇴각 검색 ) (0) | 2021.06.03 |
| [알고리즘] Dynamic Programming ( 동적 계획법 ) (0) | 2021.04.17 |