- Union Find , Disjoint Set 개념
- Union Find 과정
- Union Find 코드
Union Find라는 개념을 찾으면 항상 Disjoint Set이라는 설명이 같이 나온다.
각각의 개념에 대해서 알아보고 실제로 구현된 예제에 대해서 알아보도록 하자
Union Find ( 유니온 퐈인드)
- 상호 배타적으로 이루어진 집합을 효율적으로 표현하기 위해 만들어진 자료구조를 표현할 때 사용하는 알고리즘
여기서 말하는 "상호 배타적으로 이루어진 집합"은 "공통 원소가 없는 부분 집합"이라고 이해하면 된다.
즉, 공통 원소가 없는 부분 집합을 효율적으로 표현하기 위해 만들어진 자료구조를 표현할 때 사용하는 알고리즘이다.
보통, 여러 개의 노드가 존재할 때 두개의 노드를 선택해서, 현재 이 두 노드가 서로 같은 그래프에 속하는지 판별하는 데 사용된다.
( 아직 이해가 잘 되지 않는다면, 아래 그림을 통해서 표현하는 부분을 보면 도움 될 수도 있다)
그럼 항상 세트로 등장하는 Disjoint Set은 무엇인가
Disjoint Set ( 디스조인트 셋)
- 상호 배타적으로 이루어진 집합을 효율적으로 표현하기 위해 만들어진 자료구조
이 두 가지 정의를 보면 공통점이 있다.
"상호 배타적으로 이루어진 집합을 효율적으로 표현하기 위해 만들어진 자료구조"이다.
즉, 정리하면 Disjoint Set은 어떠한 자료구조이고, Union Find는 해당 자료구조를 표현하는 알고리즘이다.
Union Find 과정
아래 그림과 같이 여러 개의 노드가 존재한다고 해보자.
현재는 모든 노두가 서로 연결되지 않고 각자 자기 자신만을 집합의 원소로 가지고 있다.
즉, 모든 노드가 자기 자신을 가리키고 있다.
아래 표의 i는 '노드 번호', parent[i]는 '부모 노드 번호'를 의미한다 ( 자신이 어떠한 부모에 포함되어있는지를 나타냄)
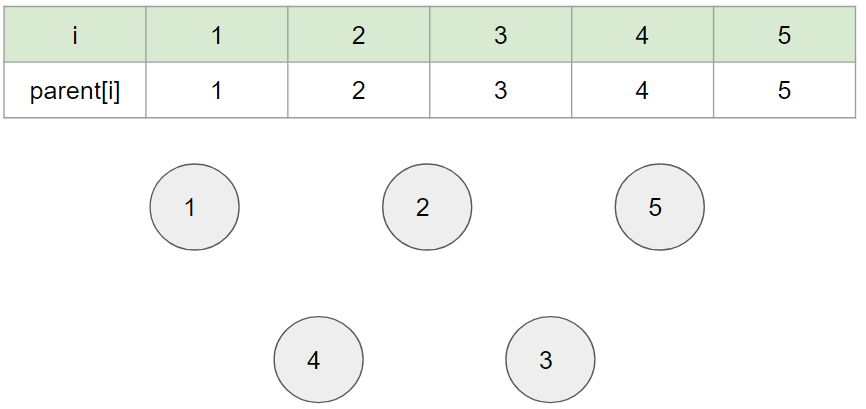
이때, Union( 1, 2 ) - 1, 2 노드를 연결하게 되면
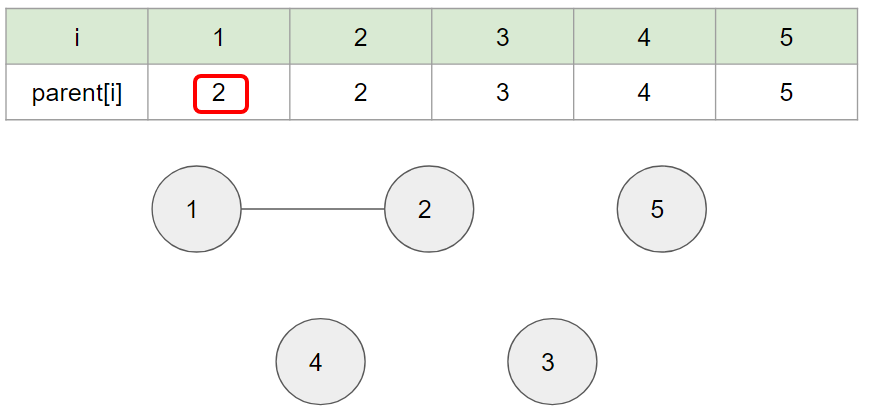
위의 그림과 같이 노드 1의 parent가 노드 2로 변경된다.
다음으로, Union( 2, 3) - 2, 3 노드를 연결 하게 되면
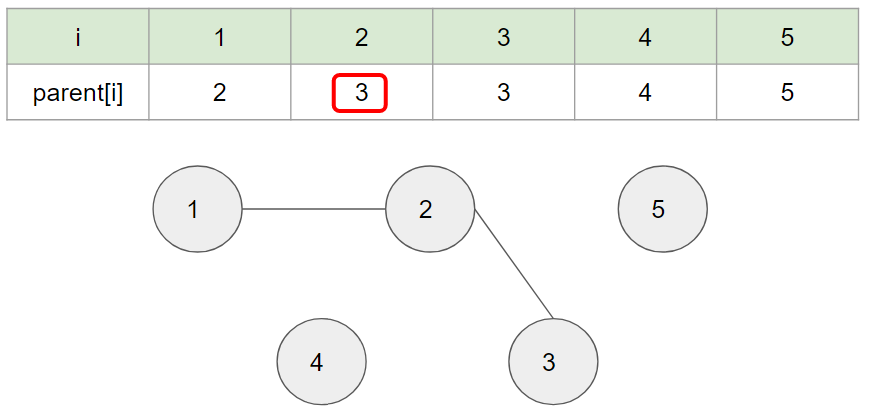
다음으로, Union( 4, 5) - 4, 5 노드를 연결 하게 되면

위와 같은 Union 함수를 호출하는 동작은 '합치기' 연산을 수행한다.
param으로 받은 노드를 연결하고 연결된 노드의 parent값을 바꾸어 주는 역할을 한다.
위에 개념에서 설명한 '공통 원소가 없는 부분 집합'은 그림에서 {1,2,3}, {4,5}에 해당한다고 이해하면 된다.
다음으로 Find 연산은 위의 각각의 원소가 어떠한 부분 집합에 속해 있는지 찾는 과정이다.
parentVal = Find ( i, parent)와 같이 노드가 어떠한 부분 집합에 속해있는지 반환해준다.
만약, 위의 예시에서 Find ( 1, parent)를 수행한다면 return 값으로는 3 값이 나온다.
( 1의 부모 2 -> 2의 부모 3 -> 3의 부모 3 (자기 자신) )
위의 내용을 정리해 보면
- make-set
- 초기화 ( parent를 자기 자신으로 지정 )
- Union(a, b)
- 합치기 ( a와 b가 속한 집합을 합친다 )
- Find ( a )
- a가 속한 집합 번호를 찾는다
Union Find 코드
private void union(int a, int b, int[] parents) {
int aParent = find(a, parents);
int bParent = find(b, parents);
if (aParent == bParent) return;
parents[aParent] = bParent;
}
private int find(int node, int[] parents) {
while(node != parents[node]) {
node = parents[node];
}
return node;
}실행 코드
public static void main(String[] args) {
int [][] edges = {{1,2}, {2,3}, {3,4}, {1,4}, {1,5}};
int [] rst = findRedundantConnection(edges);
System.out.println(Arrays.toString(rst));
}
public static int[] findRedundantConnection(int[][] edges) {
int[] parents = new int[2001];
for (int i = 0; i < parents.length; i++) { // make-set (init)
parents[i] = i;
}
for (int[] edge : edges ) {
int from = edge[0], to = edge[1];
if (find(from, parents) == find(to, parents)){ // same parent !
return edge;
}
union(from, to, parents);
}
return null;
}
'Algorithm' 카테고리의 다른 글
| [알고리즘] Backtracking ( 백트래킹, 퇴각 검색 ) (0) | 2021.06.03 |
|---|---|
| [알고리즘] Dynamic Programming ( 동적 계획법 ) (0) | 2021.04.17 |
| [알고리즘] Flood Fill ( Seed Fill ) (0) | 2021.03.27 |
| [알고리즘] BFS ( Breadth First Search ) (0) | 2021.03.27 |
| [알고리즘] DFS ( Depth First Search ) (0) | 2021.03.26 |